Jeu de Go . eu

. [ < Précédent ] .::. [ Accueil du cours sur le Yose ] .::. [ Suivant > ]

Nous avons donc étudié la technique de comptage du territoire dans de nombreuses situations, mais nous abordons ici le point vraiment central de tous ces calculs. Et pour cela, reprenons pour la troisième fois le problème A.

Problème A

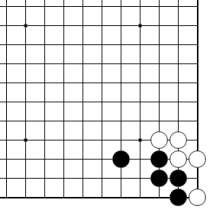
Au risque de se répéter, rappelons qu'il faut compter 1 point de territoire Noir dans l'angle du goban, mais l'essentiel est de comprendre qu'il ne s'agit pas d'un point de territoire « potentiel ». Au contraire, il faut se convaincre qu'il n'a rien de différent du simple point de territoire de la figure 29.

Figure 29

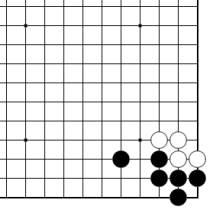
On compte 1 point de territoire dans la problème A, mais ce n'est pas seulement par commodité. Le calcul montre en fait que le problème A et la figure 29 sont exactement équivalents, et on effectue ces calculs pour soutenir le jugement...

Ce point est particulièrement difficile à saisir pour les joueurs amateurs. Même si vous parvenez à compter « 1 point de territoire noir indubitable » sur la figure 29, le problème A ne vous inspire pas confiance... Et pourtant, le territoire noir du problème A vaut lui aussi « 1 point indubitable ».

Situations équivalentes

Voici une liste de situations équivalentes qui reprennent certains des diagrammes précédents. En guise de révision, vous pouvez refaire le calcul pour comparer par vous-même.

Problème B Figure 30

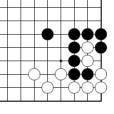
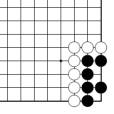
Les 2 points de territoire du problème B sont exactement identiques aux 2 points de la figure 30.

Problème C Figure 31

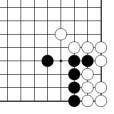
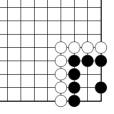
Le problème C et la figure 31 comptent tous les deux 5 points de territoire noir.

Problème E Figure 32

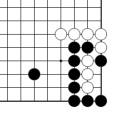
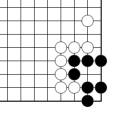
Le problème E et la figure 32 comptent 3 points de territoire noir.

Il est important de répéter encore une fois que ces valeurs issues du calcul représentent la quantité réelle de territoire noir sur chacun de ces diagrammes. Il n'existe aucune différence entre les 5 points du problème C et les 5 points de la figure 31.

Sur chacun des 4 exemples suivants, vous devez vous convaincre que les figures de gauche et de droite sont « identiques ».

problème F = figure 33 = 1 point

problème G = problème = 3 points

problème L = figure 34 = 2 points et demi

problème N = figure 35 = 5 points et demi

Problème F Figure 33

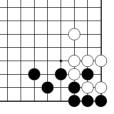
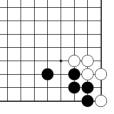
Problème G Problème I

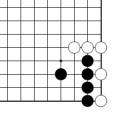
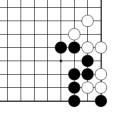
Problème L Figure 34

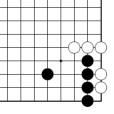
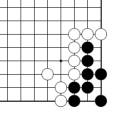
Problème N Figure 35